一橋大学の解答

文系数学では一番難しいと思います。数IIIが欲しくなる。
pdf版

各問題の解答と解説と訂正

問1

いきなりミスってますねぇ…(1)は1920ではなく100が正解です。 $10^n \mod 101$が$n\mod 4$で定まることに気づけば終わり

問2

$t=\tan{\theta}$とおいて解を求めるとうまくいく。$[0,\pi/2)\cup(\pi/2,\pi)\to\mathbb{R}$の対応は全単射になります。

問3

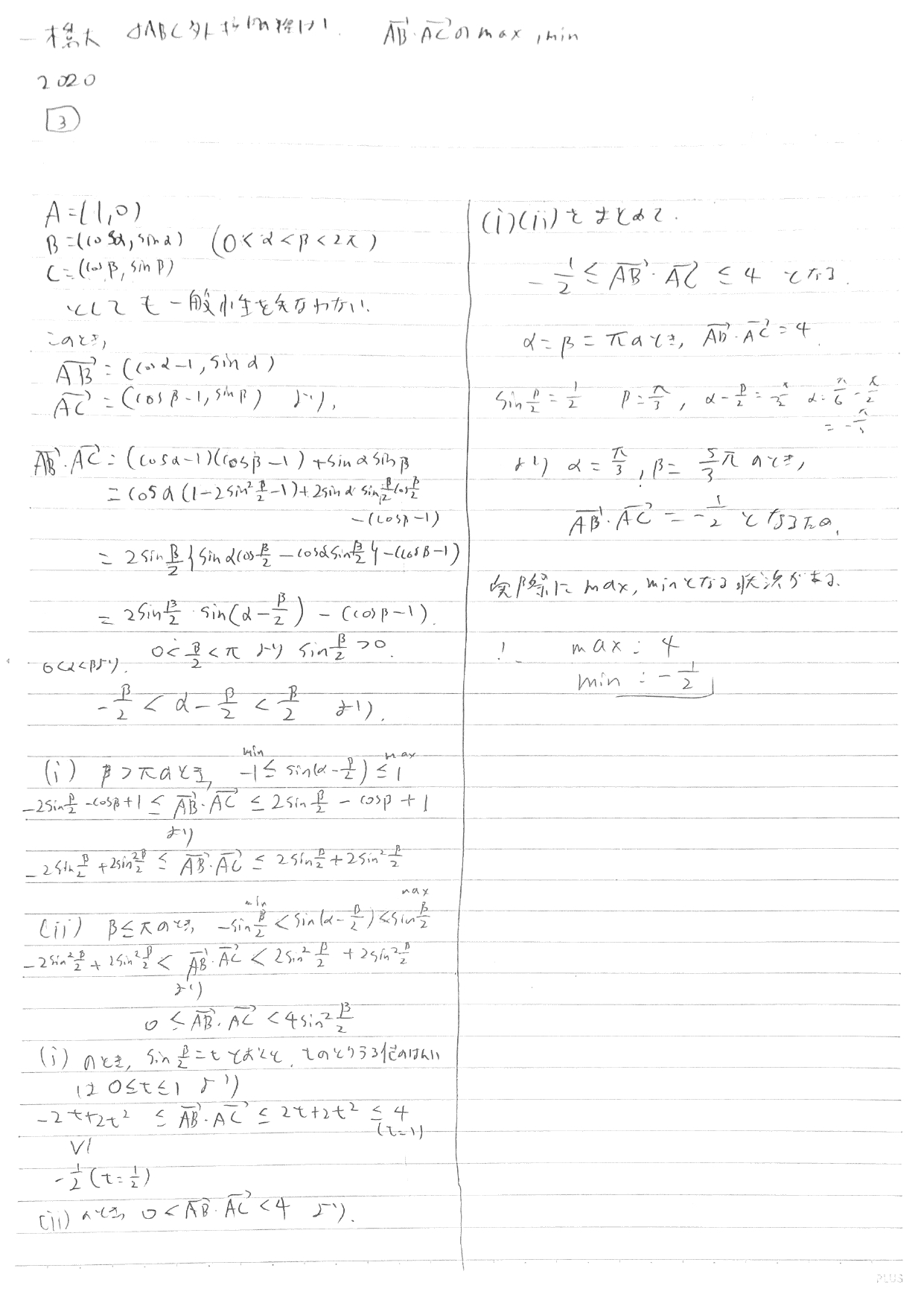
発想は楽しい問題。どこかの人がすでに作問してそうだけど。 頑張って変数の記述に落とし込んで一文字固定での最大化…これ本当に文系数学か？？？

問4

楽しい問題。$F(x)$を頑張って計算する（絶対値の挙動に注意）のはまあやるだけなのだけど、 最小化する際に実は微分しなくても良くて相加相乗平均が使えます。（この式見たら微分したいな～ってなる） 数3を知っていたら若干有利になりそうな気はする。
あと前にどっかで炎上してたけど、相加相乗平均で最小化問題を解く際には等号成立条件をチェックしなければいけない。（戒め）

問5

がんばって確率漸化式の立式をした後、$p_n$を求めずにそのまま$p_{n+1}-p_n$を求められてしまった。 たぶん$p_n$はいい感じの値に収束しそうな気はする。計算してないけど2/3あたりと睨んでいる。

---

2020年のページに戻る
解答速報のページに戻る
トップページに戻る