東京大学の解答
pdf版個人的に解いてみた感じとしての評価ですが、 1<2<4<5<6<3だと思います。3は去年問題と比べてみてもきつい。
各問題の解答と解説と訂正
問1
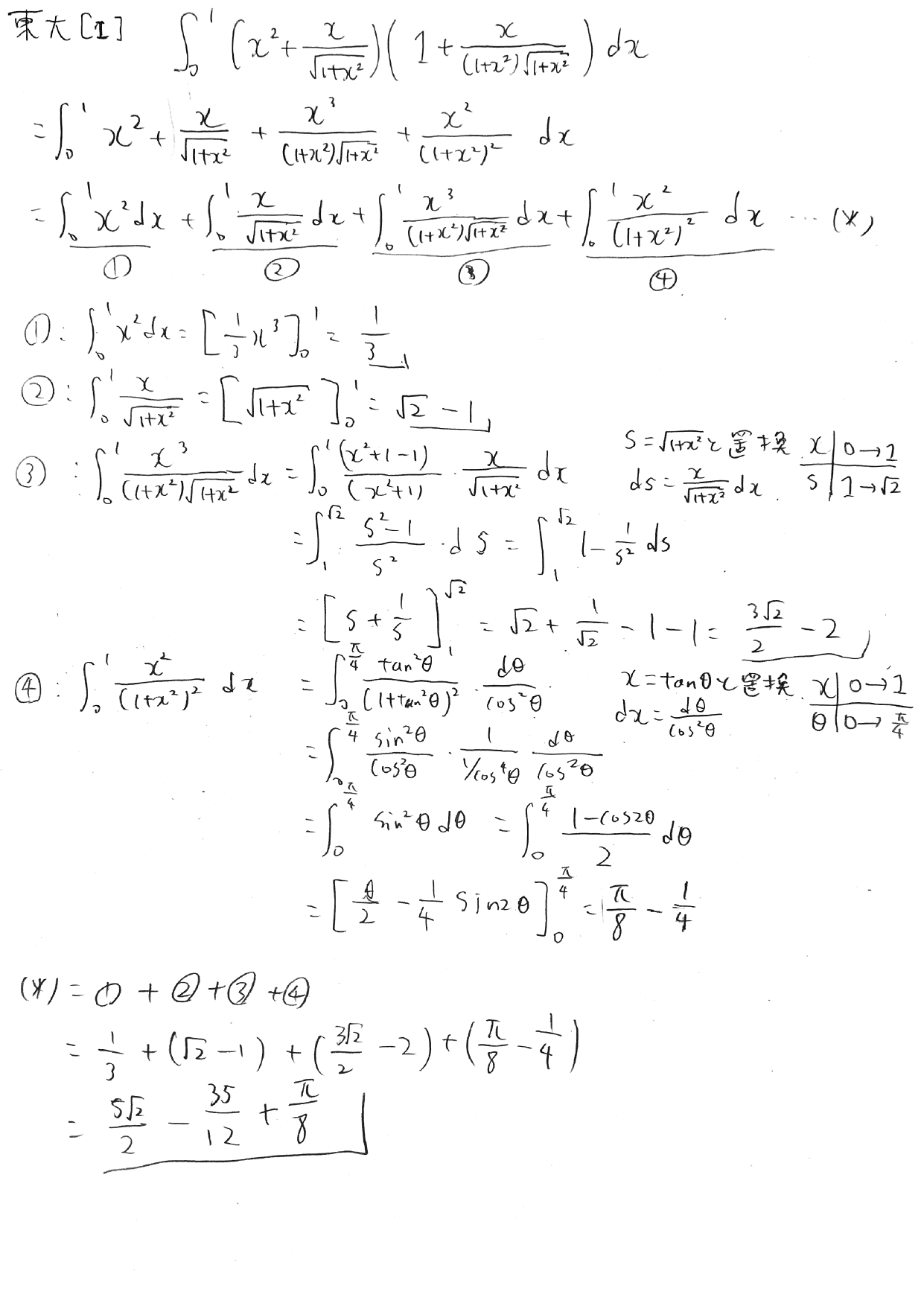
2019年東大問1はある定積分の値を求めよという問題が出てきた。 式の形が意味ありげに因数分解されているが、その意味を考察するのはほぼ無意味である。 エレガントな解き方を考察するよりも、展開して項ごとに順番に積分して足すほうが早く答えを出すことができる。 これだけ聞くとつまらない問題であるかのように聞こえるが実はそうでもない。むしろ良問の部類に入るだろう。 上記の回答を見るように、答えの各項はそれぞれ異なる方法で積分している。解き方によっては部分積分を使うこともあるが、 どのような解き方をしたとしても積分の基本的なテクニックを知らないと解くことができない。 その基本的なテクニックが身についているかをきちんと判別できるという点でも良い問題だと言えるだろう。 (というかエレガントな解き方がなかなか見つけられなかったのでなんか負けた気がしてつらい)
問2

問2は幾何学(というより図形と方程式?)と微積(数IIに収まっている?)の範囲から出題された問題である。 △APQ,△PQRの面積がそれぞれ1/3であることを利用して自由度を減らすことで一変数関数の最大最小化問題に帰着することができる。 しかしこの手の問題で気をつけなければいけないのは、必要条件と十分条件についての考察である。もし仮に値が最大となるqの値を見つけたとしても、 それに対応する点P,Q,Rが存在しない場合それを考察範囲に含めてはいけない。この問では三角形APQの面積から$\frac{2}{3}\leq q\leq 1$を満たしている必要があることがすぐに分かるが、 逆に$q$がその範囲内にある場合、条件を満たすように$0 \lt p,r \lt 1$を取ることができるかをきちんと考察しなくてはいけない。 高校数学では忘れがちだが、不等式,最大最小,取りうる値の範囲の三種類が別物であるということをきちんと理解する必要がある。
問3

問3は今回の問題セット6問の中では一番難しいだろう。(今年の東工大問4といい、難しい問題は幾何学に離散的な要素を加えたものが多い気がする) 平面と図形の切り口が多角形なのは自明(曲線がそもそもないので)だが、線分と平面との交点が頂点となるかどうか(つまり、一直線上にはならないということ)を考察したほうが議論が厳密になる。 それに場合分けが厄介で図を書くのも辛かったし、この解答もきちんと論証できてる自信がない。残念
問4

問4は整数問題。東大2019理系数学の中では個人的には一番好きな問題である。 1の誘導がうまいこと機能しているのが面白い。誘導がないとひたすらに自然数のmodを考え出して埒が明かなくなるが、 最大公約数についてのこうさつから、「$m\in\mathbb{N}$のとき、$m^2=xy$かつ$x,y$が互いに素ならば、$x,y$がともに平方数である」 という事実に気づけば話は早くなる。$n$が奇数のときは$n^2+1,5n^2+9$がともに偶数となって互いに素ではなくなるが、各因数を2で割ることで互いに素な問題に帰着できて、 最終的には平方余剰で解ける。というよりもmod5での平方余剰を知ってないと厳しいかも?このことを知らない場合どうやって論証の最後にとどめを刺すのか、気になるところである。
問5

問5はまるっきり数学IIIというような問題であった。これも問4と同じくらい好きである。ある条件によって定義された一般項がわからない数列に対しての極限である。 (1)は中間値の定理とかを使って頑張る。(2)は自明に見えるが(3)を解きやすくするための布石として機能している。 (3)については、aは(2)からほぼ自動的にわかる。bについては$a_n$の条件を吟味すれば閃くのは容易い。cはなかなか厳しくて、微分係数の極限としてみるのはよくある手法なのだが、 そこからの計算がなかなか厳しい。というか$f(x)=\sqrt{x\cos{x}}$という関数を微分したのは人生でこれが最初で最後かもしれない。 と言うものの、初見でなんかヤバそうに見える計算ほど慎重になるため案外ミスしないものである。計算ミスは気が緩んだときに起こる。
問6

問6は複素平面についての問題である。最初見たときはよくわからなくて一晩寝てから解いた問題である。条件3の$\alpha\beta+\gamma\delta$が0でない純虚数になるという制約がうまく機能している。 条件3がなければ問題はそもそも成立しないだろう。(1)についてはそもそも実数解の個数が0,2,4のどれかしかないのでそれぞれのケースを順番に潰していけばOK。 (2)については、条件3について吟味してみよう。実数にならない$\alpha$に対して、$\alpha=p+qi$というように置けば自ずと答えが見えてくる。 (3)については、文字をとことん消去すればOK。ただし条件3で「$\alpha\beta+\gamma\delta\neq 0$」を明記していることを見落とすのは良くない。 見落とすと$y=0$上の点を省き忘れることになるだろう。
2019年のページに戻る
解答速報のページに戻る
トップページに戻る